アレニウスの式と反応速度

大学で化学反応論を習うと間違いなく登場するのがこのアレニウスの式です。
高校までは「温度が高いと反応速度が速い」のような定性的な話に終始していましたが、大学からはアレニウスの式によって、理論的に話を進めることが出来るようになります。
このアレニウスの式によって、定量的な解析が行えるようになり、化学反応論をより深く理解できるようになります。

アレニウスの式の特徴

アレニウスの式は『反応速度定数k』に関する式です。
アレニウスの式には反応速度定数に関係する全てのパラメータが含まれておりとても便利です。
もし反応の『活性化エネルギー』『温度』『頻度因子』が何らかの方法で全てわかった場合、アレニウスの式を用いて反応速度を計算(※1)できることになります。
(※1 加えて、反応物のモル濃度とその反応が何次反応で進むかの情報も必要)

頻度因子A

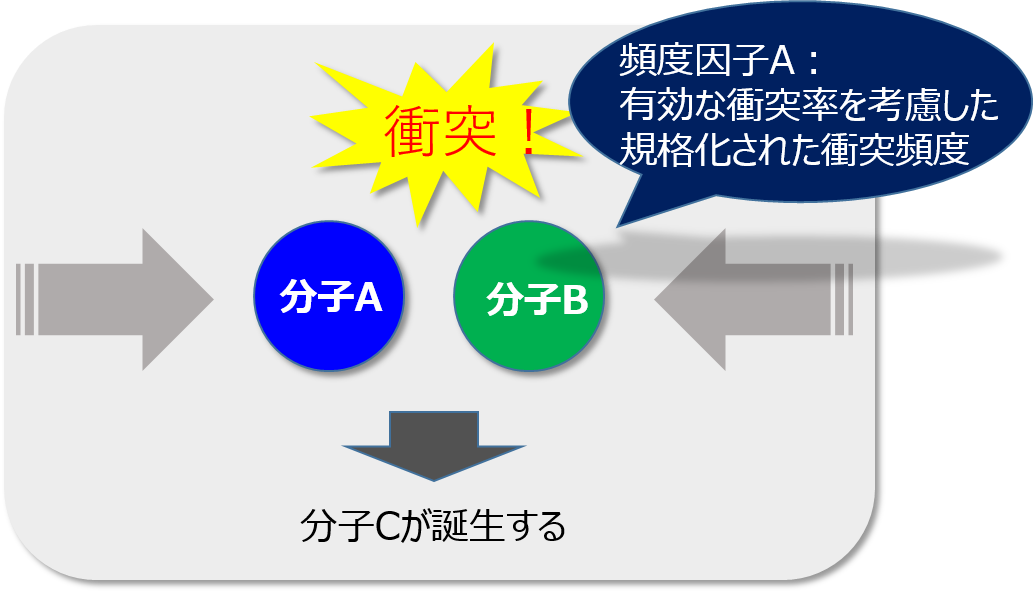
高校まであまり考えてこなかった概念ですが、反応が起こるには分子の衝突が必要になります。
この頻度因子Aというのは、単位モル濃度あたりに分子が衝突する衝突頻度Zと、有効な角度で衝突する確率を示す立体因子Pという因子を考慮した因子です。

A ＝ Z×P ＝ (規格化された分子の衝突頻度) × (有効な衝突確率)

このZというのは分子によってあまり差がないのですが、Pは分子の複雑さによって大きく異なります。
つまり、分子によって化学反応が起こるのには最適な角度があるということです。
立体障害が大きいような分子の場合は、Pは小さくなり、必然的に頻度因子Aも小さくなります。

ボルツマン因子

exp(-Ea/RT)はボルツマン因子と呼ばれる、『活性化エネルギー以上の分子の割合』を考慮した因子です。
反応は活性化エネルギー以上のエネルギーを持った分子によって起こりますが、ある温度での活性化エネルギー以上の分子の割合というのは、マクスウェル・ボルツマン分布によって計算できます。

疑問点としてよく「分子によってボルツマン分布曲線が変わるのでは？」というのがありますが、確かに“平均速度”という観点で見れば分子による違いは大きいのですが、質量などを考慮した“平均運動エネルギー( = (1/2)*mv^2 )”を考えると、どの分子も同じ曲線になります。

反応に関わるのは“平均運動エネルギー”と考えられるため、分子の種類に寄らずボルツマン因子exp(-Ea/RT)を使用することが出来るのです。

ボルツマン因子が示す通り、活性化エネルギーEaが小さいほど、また温度Tが大きいほど、exp(-Ea/RT)は大きくなり、つまり反応速度定数は大きくなります。

アレニウスの式で押さえるべき所

反応速度ではなく反応速度「定数」

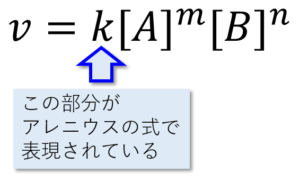
アレニウスの式は反応速度定数に関する式です。

A + B ⇔ C

という2次で進む反応があった場合、反応速度vは速度定数と濃度を掛けて、v = k[A][B]で求めます。反応速度を求めるには『濃度を掛ける』ことを忘れないでください。

反応次数はアレニウスの式ではわからない

反応速度を求めるには、速度定数kと濃度を掛け算しなければなりませんが、化学反応は2次で進行するのか2.5次で進行するのか、といった重要なことは当たり前ですがアレニウスの式からは全く分かりません。
なので、反応速度を求めるには『反応次数』もあらかじめ別の情報から知っておかなくてはならないのです。

アレニウスプロット

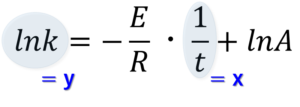
アレニウスの式に数学的に式変形(両辺に自然対数)することで、『直線』の形にすることができます。(反応速度ではなく、反応速度定数であることに注意！)

よく大学の問題演習で出されるのは、既に反応速度定数の表が与えられている場合が多いです。
それを使用してアレニウスプロットを描き、傾きから活性化エネルギーEaを求めるというのが定番です。